模电笔记-半导体二极管模型

本文为模电课程学习笔记，如有错误敬请指正

半导体二极管

二极管

二极管作为一个具单向导通特性的非线性元件，假若直接使用其伏安特性函数进行电路分析，我们将得到一个复杂且难以求解的电路方程。

因此我们需要建立一些近似模型来描述二极管的特性，这使我们得以关注于真正造成影响的电路参数。

伏安特性

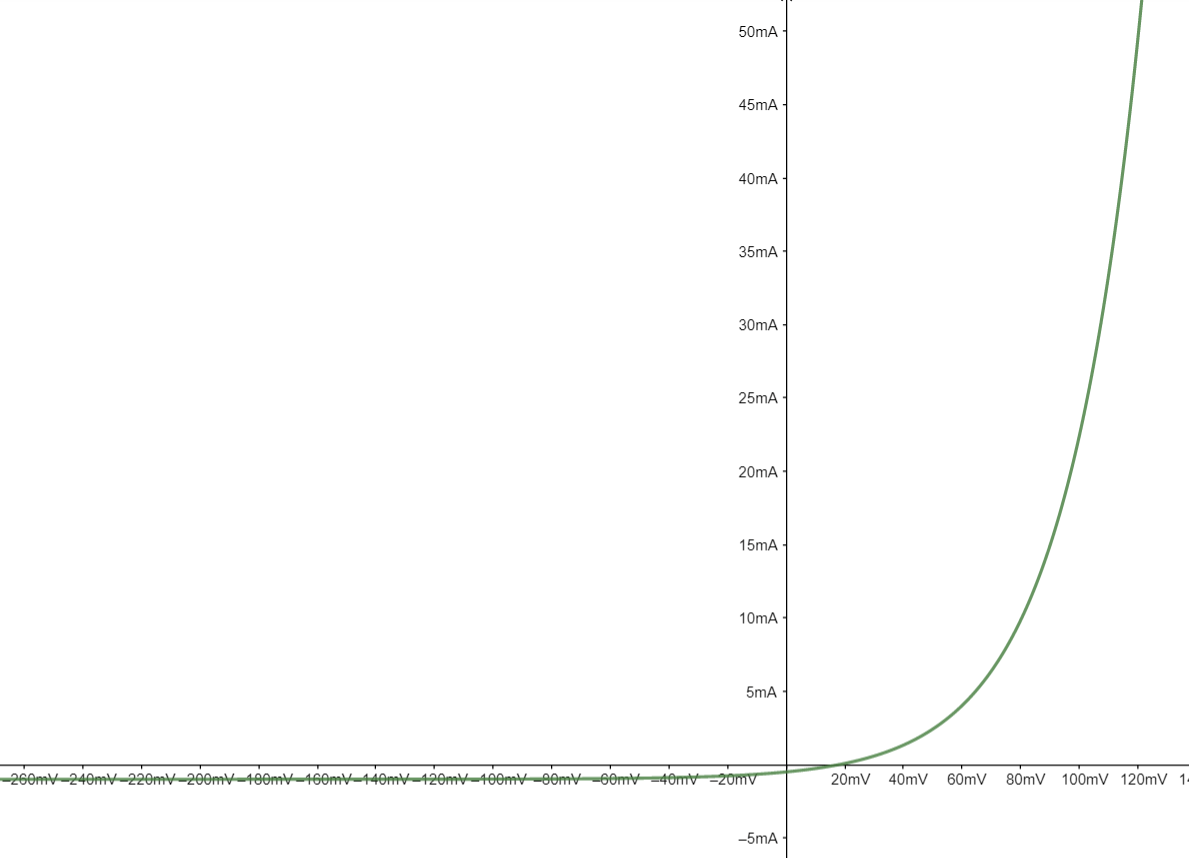
查阅相关参考书可得到二极管的伏安特性可表述为下式。

$$I=I_s(e^{\frac{U}{V_T}}-1);V_T=\frac{KT}{q}\tag{1}$$

其中$I_S$为反向饱和电流，$V_T$为熱电压，室温取26mV。

特性曲线如下图所示，我们以此图为参考，分別采用不同模型对二极管的特性进行近似。

直流分析

单向导通模型

当仅考虑二极管的单向导通特性时，如作电路的定性分析。

需放弃不必要的其他细节以得到描述导通特性的伏安曲线。

考虑二极管的正偏与反偏特性，正向电压$V$与通过电流$I$的关系进行讨论。

$$I = 0 ; V < 0 (反偏)\\I > 0 ; V> 0(正偏)$$

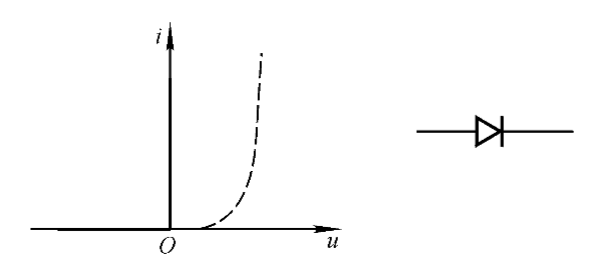
在上述近似中忽略了正向压降及截止反向电流俩个重要因素。重点反映了二极管的单向导电性，对实际电路的反映并不精确，因此仅作定性分析。

恒压源二极管模型

在实际电路中，二极管的导通特性总是在正向电压超过一定数值后才得以表现，并在导通期间表现出压降的特性，对此采用一恒流源表现正向压降特性。

$$I = 0 ; V<V_{ON}(反偏)\\I>0 ; V>V_{ON}(正偏)$$

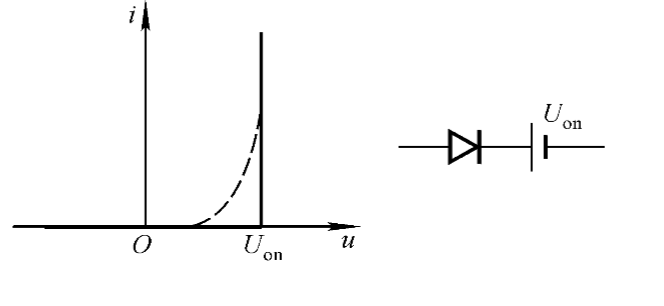
在上述近似中考虑了其单向导通及正向压降的特性，较为接近地反映了二极管的器件特性，在直流电路分析中较为常用。

折线二极管模型

一般的电路分析中，恒压源模型对二极管的近似已足够精确，若需要更为精确地考察二极管电路。则可在一定的条件下(直流小信号)，采用线性电阻近似二极管伏安特性。

$$I=0;V<V_{ON}(反偏)\\i=\frac{u-V_{ON}}{r_D};u>V_{ON}(正偏)$$

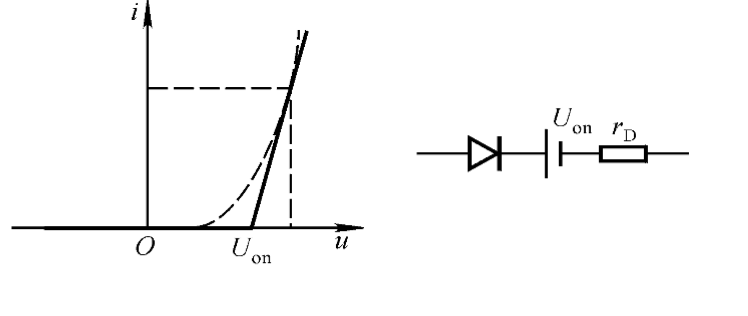
本文称此电阻为直流电阻，对于不同的近似需要，可取得不同点的$(U,I)$值用于计算出直流电阻。

附注一：折线的斜率为电阻的阻值，在电压电流单位为V和A时取$\Omega$为电阻单位。

附注二：需注意实际电流呈指数增长而折线模型仅作线性近似。

交流模型

交流小信号模型（低频）

考虑交流信号时，需注意二极管电压电流呈指数关系，非线性元件无疑提升了电路的分析难度，为简化这一过程，采用折线模型的思路进行分析。

但实际分析前，我们先提出一些条件以帮助分析。

1)电路上存在正向直流源，且电压大于导通电压。

2)交流电流的电压𡶶值远小于直流电压。

3)记直流电压及其导通电流为点$Q( U_D,I_D )$，交流电流𡶶值为$\Delta u$。

基于上述条件以及疊加定理，可以发现交流电压仅在直流电压的某一范围内波动。

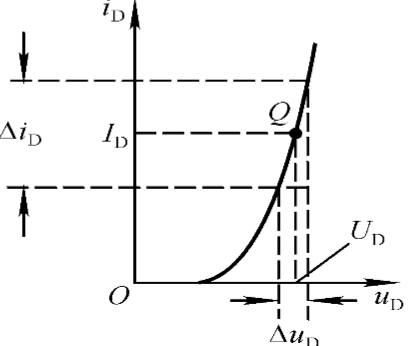
对此，如何分析i和u的变化成为了新问题，从图可见，$\Delta u$与$\Delta i$间的关系可通过折线进行近似，折线的形式为$\frac{\Delta u}{\Delta i}$，又因此关系式符合电阻特性形式，设$\frac{\Delta u}{\Delta i}=r_d$。

而交变电压足够小时，二极管电压以Q点为中心波动，范围$U\in\{ U_D - \Delta u, U_D+\Delta u\}$（疊加定理）。

考虑交流电压不断减小的过程，此时总电流趋向定值(伏安曲线连续性)，下以极限近似这一过程，重点考察折线斜率的变化。

$$\frac{1}{r_d}=\lim_{\Delta u -> 0}\frac{\Delta i}{\Delta u}=\frac{di}{du}|_{i_d=I_D}$$

考虑二极管伏安特性$I=I_s(e^{\frac{U}{V_T}}-1)$

联立俩个方程，求解解得下式。

$$\frac{1}{r_d}=\frac{di}{du}|_{i_d=I_D}=I_s \frac{1}{V_T} e^{\frac{U}{V_T}}\approx \frac{I_D}{V_T}\tag{2}$$

整理得$r_d＝\frac{V_T}{I_D}$，其中$V_T$为热电压(26mV)，$I_D$为直流点Q的电流。

这说明在固定的直流电压下，交流小信号引起的电流变化可由线性电阻近似，阻值为$r_d$。

由于二极管等效电阻这一过程可视为坐标原点的偏移，在原点偏移至直流点的过程时，电路的直流分量已被纳入计算，因此在等效后需要置零直流源，划分电路为直流电路与交流电路进行分析。

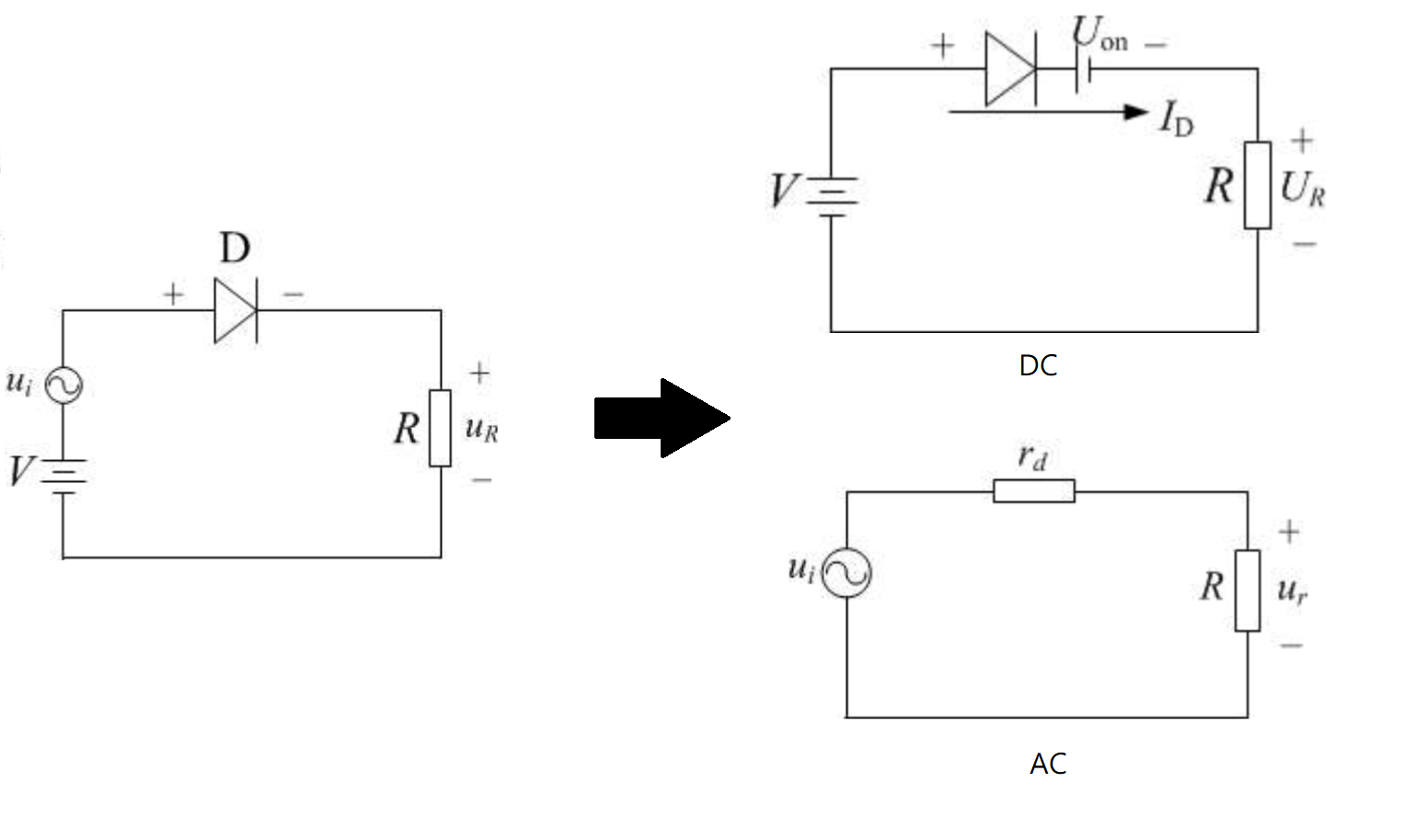
附注一：此时已采用线性元件对二极管进行近似，满足疊加定理的条件。

附注二：近似为电阻的原因为：$\frac{\Delta u}{\Delta i}$的形式与线性电阻特性方程相近，可以用线性电阻等效具有这一形式的器件，从而有$\frac{\Delta u}{\Delta i}=r_d$。

交流小信号模型（高频）

基于低频小信号模型，结合的PN结在高频时表现出的正偏扩散电容和反偏势垒电容特性。

在低频模型上进行改进，以符合高频下的器件特性。

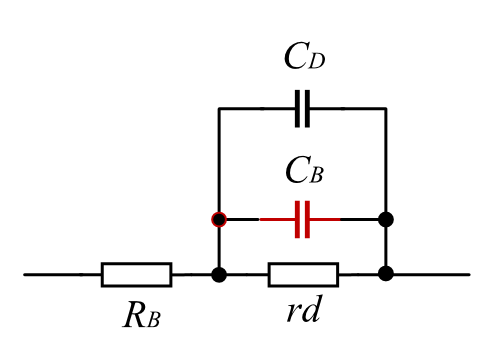
其中$C_D,C_B$分别为扩散电容及势垒电容，$R_B$为欧姆接独电阻，$r_d$为交流信号模型。

参考条目

视频：上海交通大学-郑益慧-模拟电子技术基础

书目：复旦大学-陈光梦-《模拟电子学基础》